A Nobel Prize for the Credibility Revolution
The Nobel Prize goes to David Card, Joshua Angrist and Guido Imbens. If you seek their monuments look around you. Almost all of the empirical work in economics that you read in the popular press (and plenty that doesn’t make the popular press) is due to analyzing natural experiments using techniques such as difference in differences, instrumental variables and regression discontinuity. The techniques are powerful but the ideas behind them are also understandable by the person in the street which has given economists a tremendous advantage when talking with the public. Take, for example, the famous minimum wage study of Card and Krueger (1994) (and here). The study is well known because of its paradoxical finding that New Jersey’s increase in the minimum wage in 1992 didn’t reduce employment at fast food restaurants and may even have increased employment. But what really made the paper great was the clarity of the methods that Card and Krueger used to study the problem.
The obvious way to estimate the effect of the minimum wage is to look at the difference in employment in fast food restaurants before and after the law went into effect. But other things are changing through time so circa 1992 the standard approach was to “control for” other variables by also including in the statistical analysis factors such as the state of the economy. Include enough control variables, so the reasoning went, and you would uncover the true effect of the minimum wage. Card and Krueger did something different, they turned to a control group.
Pennsylvania didn’t pass a minimum wage law in 1992 but it’s close to New Jersey so Card and Kruger reasoned that whatever other factors were affecting New Jersey fast food restaurants would very likely also influence Pennsylvania fast food restaurants. The state of the economy, for example, would likely have a similar effect on demand for fast food in NJ as in PA as would say the weather. In fact, the argument extends to just about any other factor that one might imagine including demographics, changes in tastes and changes in supply costs. The standard approach circa 1992 of “controlling for” other variables requires, at the very least, that we know what other variables are important. But by using a control group, we don’t need to know what the other variables are only that whatever they are they are likely to influence NJ and PA fast food restaurants similarly. Put differently NJ and PA are similar so what happened in PA is a good estimate of what would have happened in NJ had NJ not passed the minimum wage.
Thus Card and Kruger estimated the effect of the minimum wage in New Jersey by calculating the difference in employment in NJ before and after the law and then subtracting the difference in employment in PA before and after the law. Hence the term difference in differences. By subtracting the PA difference (i.e. what would have happened in NJ if the law had not been passed) from the NJ difference (what actually happened) we are left with the effect of the minimum wage. Brilliant!
Yet by today’s standards, obvious! Indeed, it’s hard to understand that circa 1992 the idea of differences in differences was not common. Despite the fact that differences in differences was actually pioneered by the physician John Snow in his identification of the causes of cholera in the 1840 and 1850s! What seems obvious today was not so obvious to generations of economists who used other, less credible, techniques even when there was no technical barrier to using better methods.
Furthermore, it’s less appreciated but not less important that Card and Krueger went beyond the NJ-PA comparison. Maybe PA isn’t a good control for NJ. Ok, let’s try another control. Some fast food restaurants in NJ were paying more than the minimum wage even before the minimum wage went into effect. Since these restaurants were always paying more than the minimum wage the minimum wage law shouldn’t influence employment at these restaurants. But these high-wage fast-food restaurants should be influenced by other factors influencing the demand for and cost of fast food such as the state of the economy, input prices, demographics and so forth. Thus, Card and Krueger also calculated the effect of the minimum wage by subtracting the difference in employment in high wage restaurants (uninfluenced by the law) from the difference in employment in low-wage restaurants. Their results were similar to the NJ-PA comparison.
The importance of Card and Krueger (1994) was not the result (which continue to be debated) but that Card and Krueger revealed to economists that there were natural experiments with plausible treatment and control groups all around us, if only we had the creativity to see them. The last thirty years of empirical economics has been the result of economists opening their eyes to the natural experiments all around them.
Angrist and Krueger’s (1991) paper Does Compulsory School Attendance Affect Schooling and Earnings? Is one of the most beautiful in all of economics. It begins with a seemingly absurd strategy and yet in the light of a few pictures it convinces the reader that the strategy isn’t absurd but brilliant.
The problem is a classic one, how to estimate the effect of schooling on earnings? People with more schooling earn more but is this because of the schooling or is it because people who get more schooling have more ability? Angrist and Krueger’s strategy is to use the correlation between a student’s quarter of birth and their years of education to estimate the effect of schooling on earnings. What?! What could a student’s quarter of birth possibly have to do with how much education a student receives? Is this some weird kind of economic astrology?
Angrist and Krueger exploit two quirks of US education. The first quirk is that a child born in late December can start first grade earlier than a child, nearly the same age, who is born in early January. The second quirk is that for many decades an individual could quit school at age 16. Put these two quirks together and what you get is that people born in the fourth quarter are a little bit more likely to have a little bit more education than similar students born in the first quarter. Scott Cunningham’s excellent textbook on causal inference, The Mixtape, has a nice diagram:

Putting it all together what this means is that the random factor of quarter of birth is correlated with (months) of education. Who would think of such a thing? Not me. I’d scoff that you could pick up such a small effect in the data. But here come the pictures! Picture One (from a review paper, Angrist and Krueger 2001) shows quarter of birth and total education. What you see is that years of education are going up over time as it becomes more common for everyone to stay in school beyond age 16. But notice the saw tooth pattern. People who were born in the first quarter of the year get a little bit less education than people born in the fourth quarter! The difference is small, .1 or so of a year but it’s clear the difference is there.
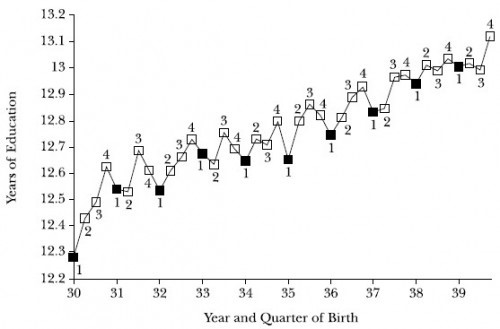
Ok, now for the payoff. Since quarter of birth is random it’s as if someone randomly assigned some students to get more education than other students—thus Angrist and Krueger are uncovering a random experiment in natural data. The next step then is to look and see how earnings vary with quarter of birth. Here’s the picture.

Crazy! But there it is plain as day. People who were born in the first quarter have slightly less education than people born in the fourth quarter (figure one) and people born in the first quarter have slightly lower earnings than people born in the fourth quarter (figure two). The effect on earnings is small, about 1%, but recall that quarter of birth only changes education by about .1 of a year so dividing the former by the latter gives an estimate that implies an extra year of education increases earnings by a healthy 10%.
Lots more could be said here. Can we be sure that quarter of birth is random? It seems random but other researchers have found correlations between quarter of birth and schizophrenia, autism and IQ perhaps due to sunlight or food-availability effects. These effects are very small but remember so is the influence of quarter of birth on earnings so a small effect can still bias the results. Is quarter of birth as random as a random number generator? Maybe not! Such is the progress of science.
As with Card and Kruger the innovation in this paper was not the result but the method. Open your eyes, be creative, uncover the natural experiments that abound–this was the lesson of the credibility revolution.
Guido Imbens of Stanford (grew up in the Netherlands) has been less involved in clever studies of empirical phenomena but rather in developing the theoretical framework. The key papers are Angrist and Imbens (1994), Identification and Estimation of Local Treatment Effects and Angrist, Imbens and Rubin, Identification of Causal Effects Using Instrumental Variables which answers the question: When we use an instrumental variable what exactly is it that we are measuring? In a study of the flu, for example, some doctors were randomly reminded/encouraged to offer their patients the flu shot. We can use the randomization as an instrumental variable to measure the effect of the flu shot. But note, some patients will always get a flu shot (say the elderly). Some patients will never get a flu shot (say the young). So what we are really measuring is not the effect of the flu shot on everyone (the average treatment effect) but rather on the subset of patients who got the flu shot because their doctor was encouraged–that latter effect is known as the local average treatment effect. It’s the treatment effect for those who are influenced by the instrument (the random encouragement) which is not necessarily the same as the effect of the flu shot on groups of people who were not influenced by the instrument.
By the way, Imbens is married to Susan Athey, herself a potential Nobel Prize winner. Imbens-Athey have many joint papers bringing causal inference and machine learning together. The Akerlof-Yellen of the new generation. Talk about assortative matching. Angrist, by the way, was the best man at the wedding!
A very worthy trio.