Do Awards Reduce Productivity?
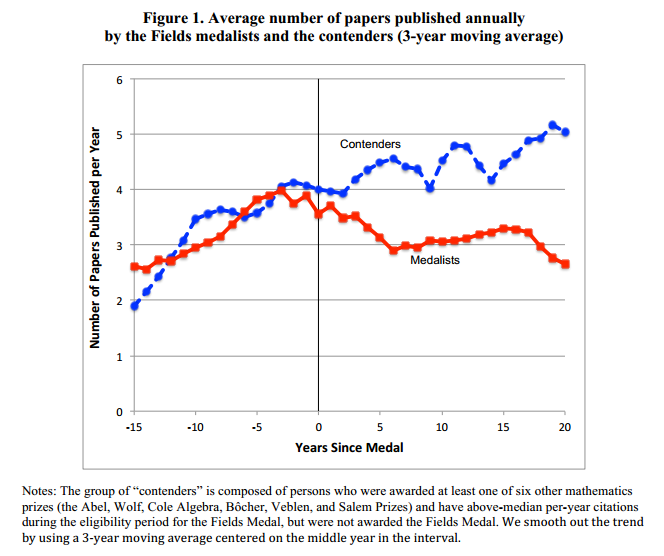 George J. Borjas and Kirk B. Doran find that the productivity of mathematicians who win the Fields Medal, the mathematics “Nobel” awarded to mathematicians under the age of 40, declines after they win. Borjas and Doran look at productivity on a number of margins including papers, citations, and graduate students mentored. At right is a graph of average number of papers compared to a contender group. Productivity falls by a statistically significant ~1 paper per year (in the regression that I think the strongest, in a few variants the decline is a bit more.)
George J. Borjas and Kirk B. Doran find that the productivity of mathematicians who win the Fields Medal, the mathematics “Nobel” awarded to mathematicians under the age of 40, declines after they win. Borjas and Doran look at productivity on a number of margins including papers, citations, and graduate students mentored. At right is a graph of average number of papers compared to a contender group. Productivity falls by a statistically significant ~1 paper per year (in the regression that I think the strongest, in a few variants the decline is a bit more.)
Not all of the decline is due to resting on laurels. Borjas and Doran also find that mathematicians who win the Fields tend to branch out into other areas and this branching out requires them to learn new material which takes time. Steve Smale did work in economics and biology, for example, Rene Thom developed catastrophe theory and David Mumford works in vision and pattern theory. Exploring new topics can also lead to breakthroughs so branching out is not necessarily a negative effect. Borjas and Doran estimate that about half of the productivity effect is resting on laurels and half greater exploration.
(FYI, Borjas and Doran speak of prizes but I prefer to call them awards because awards such as the Fields or Clark Medal are quite different from prizes for purpose, such as the XPrizes, the H Prize or the historically important Orteig Prize, that I discuss in Launching as alternatives to patents.)
Winning the Fields is presumably good for the winner but even taking into account the enhanced incentive to explore it’s not obviously good for mathematics. The explicit purpose of the Fields was to increase not decrease achievement. What can be done?
The Fields Medal may be too important for its own good. In economics the closest thing to the Fields is the John Bates Clark award, given to that American economist under the age of 40 judged to have made the most significant contributions. Chan et al. (2013) find that recipients of the Clark award increase their productivity after winning. But the Clark award is widely seen as a future portent of the Nobel, thus it may have a more stimulative effect as the winner realizes that the next big award is within reach (see the final sentence). In a tournament, it’s important to tier the awards for multiple levels of ability.
In thinking about whether awards increase or decrease productivity on net. the precise counter-factual is important. Let us accept as Truth that winners of the Fields Medal decrease in productivity, even so that doesn’t mean that eliminating the Fields Medal would increase productivity let alone that eliminating all awards would increase productivity (remember, the productivity of the contenders may be more important than the productivity of the winners). Perhaps the most justifiable policy recommendation is that one shouldn’t give awards to young people, a Fields Medal for lifetime achievement, much as the economics Nobel is given, might encourage more achievement.
Paul Samuelson wrote of Chasing the Bitch Goddess of Success:
Scientists are as avaricious and competitive as Smithian businessmen. The coin they seek is not apples, nuts, and yachts; nor is it the coin itself, or power as that term is ordinarily used. Scholars seek fame.
But, paraphrasing Tyler, what price early fame?