COVID-19 Event Risk Assessment Planner
The mathematics for calculating the probability of exposure given the number of carriers in a population and group size aren’t difficult but they can be surprising. Even a low number of carriers can generate a relatively high probability for reasonably sized groups. For example, assume you run a firm of 1000 people in the San Francisco Bay Area (population 8 million.) Let’s suppose that there are just 500 carriers in the area. In this case, assuming random draws, the probability that at least one of your employees is a carrier is 6%. You can run your own calculations at Wolfram Alpha following this format:
p=8000000, c=500, g=1000, 1-1(1-c/p)^g //N
where p is the population size, c is the number of carriers, g is the group size and the //N at the end isn’t a division but a command to Wolfram Alpha to give you a numerical answer.
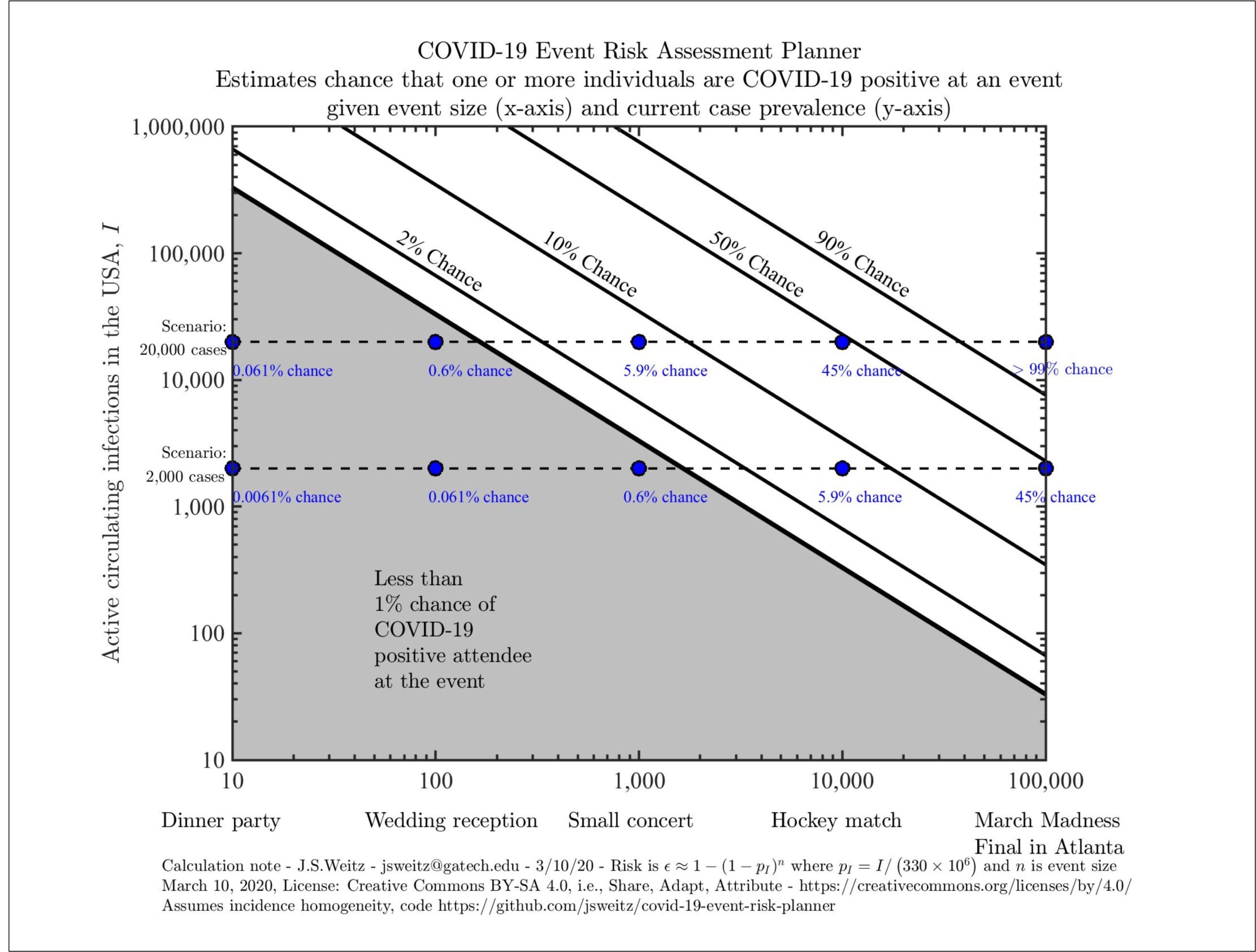
Joshua Weitz on twitter put together this graphic using the same calculations but for the United States as a whole (population 330 million). It says, for example, that if there are 20,000 carriers in the United States then at a small concert of 1000 people there is a 5.9% chance of at least one carrier attending. At the March Madness final in Atlanta with 100,000 attendees there is a greater than 99% chance that at least one attendee is a carrier.
Now here is the most important point. It’s the size of the group, not the number of carriers that most drives the result. For example, suppose our estimate of the number of carriers if off by a factor of 10–that is instead of 20,000 there are just 2000 carriers in the United States. In this case, the probability of at least one carrier at a big event of 100,000 drops not by a factor of ten but just to 45%. In other words, large events are a bad idea even in scenarios with just a small number of carriers.