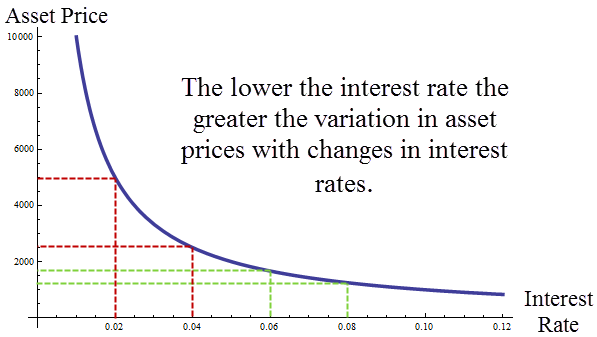
Asset Prices and Interest Rates
There has been a lot of discussion recently of Fed policy, tapering, and asset price “bubbles.” One point to bear in mind is that when interest rates are low even rationally determined asset prices may fluctuate wildly. Consider, the simplest Gordon model of asset prices in which future dividends are expected to be $100 forever, then the asset price is $100/r where r is the interest rate. If r is .1, for example, then the stock will be worth $1000. At an interest rate of 10% the price of an asset that pays $100 forever is just $1000 because the future is heavily discounted. If the interest rate were to fall to 9%, the asset price would rise to 1111.11 ($100/.09). The asset is worth more at a lower interest rate because the future counts for more but not that much more since the far future is still discounted to near zero. On the other hand, if the interest rate were .02 the asset would be worth $5000, much more since the future is discounted less heavily. Most importantly, notice that if the interest rate were to fall the same amount as before to .01 then the asset price doubles to $10,000. Thus, when interest rates are low we can expect very wide swings in asset prices. The figure illustrates:
The Gordon model is simple, of course, but adding other factors such as possible variations in dividend growth rates tends to reinforce the conclusion. At low interest rates, for example, even small variations in dividend growth rates will also generate large swings in asset prices.
The lesson is that QE doesn’t have to generate bubbles to generate wide swings in asset prices it just has to lower interest rates.