More on Bartels
I’m a little surprised that the Bartels result is receiving so much attention because the result, in slightly different form, has long been known to political economists under the rubric of partisan business cycle theory. In a nutshell, the theory of partisan business cycles says that Democrats care more about reducing unemployment, Republicans care more about reducing inflation. Wage growth is set according to expected inflation in advance of an election. Since which party will win the election is unknown wages growth is set according to a mean of the Democrat (high) and Republican (low) expected inflation rates. If Democrats are elected they inflate and real wages fall creating a boom. If Republicans are elected they reduce inflation and real wages rise creating a bust. Notice that in PBC theory neither party creates a boom or bust it’s uncertainty which drives the result – if the winning party were known there would be neither boom nor bust.
Ok, there’s plenty to question about the theory but let’s look at the data.
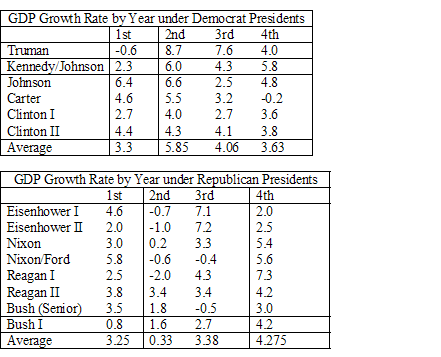
Notice that in the second year of just about every Democratic Presidency there is a boom. Interestingly, the boom is biggest for Truman whose reelection was highly uncertain (remember Dewey wins!) thus expected inflation would have been low and the boom big. Similarly the boom is smallest (relative to the surrounding years) for Clinton II a relatively certain reelection.
Now look at Republicans in just about every second year of a Republican Presidency there is a bust. The one major exception being Reagan II where uncertainty about the outcome was low.
It’s pretty clear that this result can explain Bartels’s result which is exactly Tyler’s point in his post. It’s equally clear that when we consider Presidents there aren’t many data points. (PBC does appear to hold somewhat in other countries).
Notice that the reason for the result, according to PBC, is sticky wages and the business cycle and not some nefarious story about taxes, oligarchies and political conspiracies.
