Average is Over
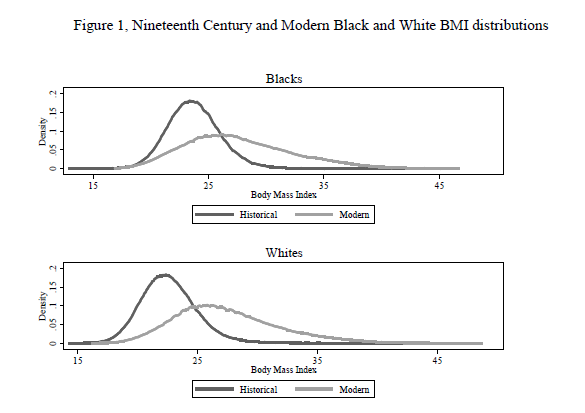
There has been an increase in the mean body-mass index since the 19th century but even more strikingly there has been an increase in the variance, what we might call an increase in weight inequality. More here.
Hat tip: Andrew Leigh.