Depreciating Capital
Brad DeLong attacks Krusell and Smith for using in some of their thought experiments a depreciation rate of 10%, which is probably too high. Fair point but in my post I assumed a depreciation of just 5% and showed that Solow and Piketty give very different predictions about how the K/Y ratio will change with a change in g.
Furthermore, having read DeLong’s comment, I went to the BEA and compared gross and net domestic product which gives capital depreciation as a fraction of GDP of around 15% in recent decades. At a K/Y ratio of 4 that’s a depreciation rate of 3.75%. Similarly, Inklaar and Timmer in constructing capital stocks for the Penn World Tables estimate a depreciation rate for the U.S. of 4.1%. I reran my simple Excel chart with the lower number, 3.75%.
As you can see, the numbers are very similar to earlier and the key point is still that a decrease in g increases K/Y much more in the Piketty model than in the Solow model. 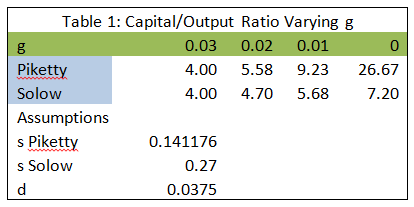 Krusell responds to DeLong here making the additional point that their thought experiments show that Piketty’s assumption about savings is implausible at any depreciation rate (see also Hamilton on this point).
Krusell responds to DeLong here making the additional point that their thought experiments show that Piketty’s assumption about savings is implausible at any depreciation rate (see also Hamilton on this point).
First: if the net rate of saving remains positive as the economy’s growth rate falls toward zero, as Piketty assumes in his second fundamental law of capitalism, the gross saving rate in the economy must approach 100%. This observation is a way of illustrating how unreasonable the behavioral assumptions underlying his theory of saving really are.
Second: according to standard, and much more reasonable, saving theory (based either on the standard textbook Solow growth model or on the permanent-income model), the net saving rate must fall with the rate of growth, and become zero when growth is zero.
…These points are key because Piketty’s predictions are all about what happens as growth falls during the 21st century, as he argues it will.
…both of these results hold no matter what the depreciation rate is (so long as it is positive).
The heart of Piketty’s theory is his expression for the capital share of income in the long run, α = r × s/g with the prediction that if g falls the capital share will rise tremendously. This is a good opportunity to summarize some of the recent points about the theory.
There are no contradictions but many a slip ‘twixt the cup and the lip. Namely, will g fall? If g does fall, will K/Y increase? If K/Y increases will capital’s share of income increase? My answers:
Will g fall? Uncertain. Piketty’s forecast is as good as anyone’s. My own view is that at the global level g has been increasing for several centuries and that this will continue, especially because in this century we will see a massive increase in the number of scientists and engineers as China and then India devote increased human capital to the research frontier.
If g does fall, will K/Y increase? Yes, but probably less than Piketty estimates and more in line with Solow.
If K/Y increases will capital’s share of income increase? Uncertain but more likely no than yes. It depends on the elasticity of substitution between K and L and as Rognlie and Summers argue, the elasticity that Piketty needs is higher than current estimates suggest is the case.