The Frechet Probability Bounds — Super Wonky!

I recently ran across a problem using the Frechet probability bounds. The bounds weren’t immediately obvious to me and Google didn’t enlighten so I wrote an intuitive explanation. Super wonkiness to follow. You have been warned.

Suppose that we have two events A and B which occur with probability P(A) and P(B). We are interested in saying something about the joint event P(A∩B), the probability that both events occur, but we don’t know anything about whether the events are correlated or independent. Can we nevertheless say something about the joint event P(A∩B)? We can. The Frechet bounds or inequalities tell us:

max[0,P(A)+P(B)-1] ≤ P(A∩B) ≤ min[P(A),P(B)]

In words, the probability of the joint event can’t be smaller than max[0,P(A)+P(B)-1] or bigger than min[P(A),P(B)]. Let’s give an intuitive explanation.

The events themselves are not important only the probabilities so let’s use an intuitive model for the events. Let x be a random number distributed between 0 and 1 with each number equally likely (i.e. a uniform distribution). Suppose that the event A occurs whenever x is in some region between a and b. For example, we might say that event A occurs if x is between .4 and .6 and event B occurs if x is between .1 and .7. Notice also that since any number between 0 and 1 is equally likely the probability that event A occurs is just the width of the A region, b-a. In this case, for example, P(A)=.6-.4=.2 and similarly P(B)=.7-.1=.6.

Now suppose that a demon arranges the events A and B to minimize the probability that both events occur. What is the smallest the demon could make P(A∩B)? To minimize the probability that both A and B occur we can think of the demon as placing the two events “as far apart” as possible. For example, the demon will begin one event at 0 and define it as the region moving right until the width is equal to P(A) and the other event the demon will begin at 1 and move left until the width is equal to P(B). If P(A)=.2 and P(B)=.4, for example, then the demon will define the events so that A∈[0,.2] and B∈[.6,1]. Here’s a picture. Notice that by beginning one event at 0 and the other at 1 the demon minimizes the overlap which is the probabiity that both events occur.

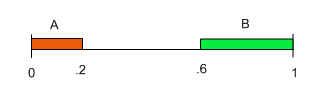In this case, the events don’t overlap at all and so the demon has ensured that the probability of P(A∩B)=0.

But what if the two events must overlap? Suppose for example that P(A)=.5 and P(B)=.7 then the demon’s logic of minimization leads to the following picture:

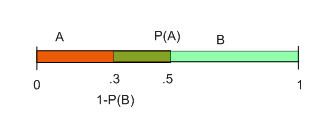We can see from the picture that the overlap is the region between .3 and .5 which we know has probability .5-.3=0.2. Thus we have discovered that if P(A)=.5 and P(B)=.7 then the joint probability has to be at least .2, i.e. .2≤P(A∩B).

Now let’s generalize. The probability of any event occuring is the length of its region b-a but since the demon always begins the event A at 0 then the probability of P(A) is simply b the rightmost point of the A region. Thus, on the diagram the rightmost point of the A region is labelled P(A) (.5 in this case). Also since the demon always begins the B region at 1, P(B)=1-a′ where a′ is the leftmost point of the B region so rearranging we have that the leftmost point a′=1-P(B) as shown in the picture at .3. Thus, we can read immediately from the figure that the overlap region has length P(A)-(1-P(B)). Notice that if P(A)<1-P(B) then there is no overlap and the difference is a negative number. Rearranging slightly, the length of the overlap region is P(A)+P(B)-1. So now we have two cases, either there is no overlap at all in which case P(A∩B)=0 or there is overlap and P(A∩B)=P(A)+P(B)-1. So putting it all together we have proven that:

max[0,P(A)+P(B)-1] ≤ P(A∩B)

The Frechet bounds also say:

P(A∩B) ≤ min[P(A),P(B)]

This is much easier to show. If minimization is accomplished by minimizing the overlap then maximization is accomplished by maximizing the overlap. To maximize the joint probability the demon starts both regions at the same point, say at the 0 point, so the picture looks like this:
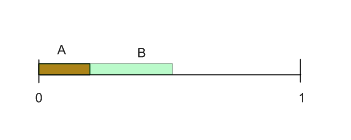The joint probability is then the region of overlap. But the regions can’t overlap by more than the smallest of the two regions! In this case the A region is smaller than the B region and since the regions start at 0 we have P(A∩B)≤P(A). Generalizing we have that:

P(A∩B) ≤ min[P(A),P(B)]

Thus we have proven the Frechet bounds:

max[0,P(A)+P(B)-1] ≤ P(A∩B) ≤ min[P(A),P(B)]

Addendum: Here is Heckman on the theory of Frechet Bounds and Heckman and Smith and Heckman, Smith and Clements with applications.