The Performance Pay Nobel
The Nobel Prize in economics goes to Oliver Hart and Bengt Holmstrom for contract theory, the design of incentives. See Tyler’s posts below for overviews. In our textbook, Modern Principles, Tyler and I have a chapter called Managing Incentives which covers some of this work, especially related to Holmstrom’s work on performance pay. Let’s give a simplified precis (fyi, the textbook doesn’t have the math).
Suppose that you are a principal monitoring an agent who produces output. The output depends on the agent’s effort but also on noise. It wouldn’t be a very efficient contract to just reward the agent based on output since then you would mostly be responding to noise—punishing hard-working agents when the noise factors were bad and rewarding lazy agents when the noise factors were good. Not only is that unfair–if you setup a contract like this the agents will a) demand that you pay them a lot of money in the good state because they will be taking on a lot of risk and b) the agents won’t put in much effort anyway since their effort will tend to be overwhelmed by the noise, either good or bad. Thus, rewarding output alone gets you the worst of all worlds, you have to pay a lot and you don’t get much effort.
But perhaps in addition to output, y, you have a signal of effort, call it s. Both y and s signal effort with noise but together they provide more information. First, lesson – use s! In fact, the informativeness principle says you should use any and all information that might signal the agent’s effort in developing your contract. But how should you combine the information from y and s? Suppose you write a contract where the agent is paid a wage, w=B0+By*y+Bs*s where Bo is the base wage, By is the beta on y, how much weight to put on output and Bs is the weight on the s signal–think of By as the performance bonus and Bs as a subjective evaluation bonus. Then it turns out (under some assumptions etc. Canice Prendergast has a good review paper) you should weight By and Bs according to the following formula:
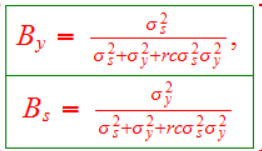
that looks imposing but it’s really not. σ^2s (sorry for the notation) is the variance of the s signal, σ^2y is the variance of the y signal. Now for the moment assume r is zero so the formula boils down to:
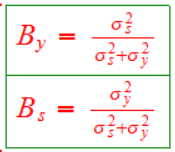
Ah, now that looks sensible because it’s an optimal information theorem. It says that you should put a high weight on y when the s signal is relatively noisy (notice that By goes to 1 as σ^2s increases) and a high weight on s when the y signal is relatively noisy. Notice also that the two betas sum to 1 which means that in this world you put all the risk on the agent. Ok, now let’s return to the first version and fill in the details. What’s r? r is a measure of risk aversion for the agent. If r is zero then the agent is risk neutral and we are in the second world where you put all the risk on the agent. If the agent is risk averse, however, then r>0 and so what happens? If r>0 then you don’t want to put all the risk on the agent because then the agent will demand too much so you take on some risk yourself and tamp down By and Bs (notice that the bigger is r the smaller are both By and Bs) and instead increase the base wage which acts as a kind of insurance against risk. So the first version combines an optimal information aggregation theorem with the economics of managing the risk-performance-pay tradeoff.
(c, by the way, is a measure of how costly effort is to the agent and so it also makes sense that the higher is c the less weight you put on performance incentives and the more on the base wage.)
Let’s also discuss some further work which is closely related to Holmstrom’s approach, tournament theory (Lazear and Rosen). When should you use absolute pay and when should you use relative pay? For example, sometimes we reward salespeople based on their sales and sometimes we reward based on which agent had the most sales, i.e. a tournament. Which is better? The great thing about relative pay is that it removes one type of noise. Suppose, for example, that sales depend on effort but also on the state of the economy. If you reward based on absolute sales then you are rewarding a lot of noise. Once again, that has two bad effects it means that you have to pay your agents a lot since you are imposing risk on them and it means that they won’t work that hard since they know they will be paid a lot when the economy is good and hardly at all when the economy is bad so in neither case do the agents have strong incentives to work hard. Suppose, however, that you have a relative pay scheme, a tournament. Now you have removed the noise coming from the state of the economy–since all the salespeople face the same economy and since there is always a first, second and third place the agent’s now have an incentive to work hard in good or bad times. Not only do they have an incentive to work hard you don’t have to pay them much of a risk premium since more of their pay is now based on their own effort rather than on noise.
But relative pay isn’t always better. If the sales agents come in different ability levels, for example, then relative pay means that neither the high ability nor the low ability agents will work hard. The high ability agents know that they don’t need to exert high effort to win and the low ability agents know that they won’t win even if they do exert high effort. Thus, if there is a lot of risk coming from agent ability then you don’t want to use tournaments. Or to put it differently, tournaments work best when agent ability is similar which is why in sports tournaments we often have divisions (over 50, under 30) or rounds.
FYI, in our textbook Tyler and I use this model to discuss when students should prefer an absolute grading scale and when they should prefer grading on a curve. Work it out!
Holmstrom’s work has lot of implications for structuring executive pay. In particular, executive pay often violates the informativeness principle. In rewarding the CEO of Ford for example, an obvious piece of information that should used in addition to the price of Ford stock is the price of GM, Toyota and Chrysler stock. If the stock of most of the automaker’s is up then you should reward the CEO of Ford less because most of the gain in Ford is probably due to the economy wide factor rather than to the efforts Ford’s CEO. For the same reasons, if GM, Toyota, and Chrysler are down but Ford is down less then you might give the Ford CEO a large bonus even though Ford’s stock price is down. Oddly, however, performance pay for executives rarely works like a tournament. As a result, CEOs are often paid based on noise.
The basic framework has since been applied in many different circumstances because principal-agent can be interpreted in many different ways employer-worker, teacher-student, regulator-banker and so forth. Thus the basic insights have been reflected in a wealth of applications each of which adds to the body of theory.