AIs Quickly Learn to Collude
AI’s are better than humans at Chess and Go, why shouldn’t they also be better at the game of collusion? Calvano, Calzolari, Denicolò and Pastorello show that they are (here quoting a VOXEU summary by the authors):
[In Calvano et al. 2018a] we construct AI pricing agents and let them interact repeatedly in controlled environments that reproduce economists’ canonical model of collusion, i.e. a repeated pricing game with simultaneous moves and full price flexibility. Our findings suggest that in this framework even relatively simple pricing algorithms systematically learn to play sophisticated collusive strategies. The strategies mete out punishments that are proportional to the extent of the deviations and are finite in duration, with a gradual return to the pre-deviation prices.
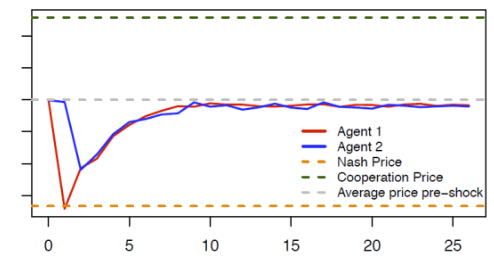
Figure 1 illustrates the punishment strategies that the algorithms autonomously learn to play. Starting from the (collusive) prices on which the algorithms have converged (the grey dotted line), we override one algorithm’s choice (the red line), forcing it to deviate downward to the competitive or Nash price (the orange dotted line) for one period. The other algorithm (the blue line) keeps playing as prescribed by the strategy it has learned. After this exogenous deviation in period , both algorithms regain control of the pricing.
Figure 1 Price responses to deviating price cut
Note: The blue and red lines show the price dynamic over time of two autonomous pricing algorithms (agents) when the red algorithm deviates from the collusive price in the first period.
The figure shows the price path in the subsequent periods. Clearly, the deviation is punished immediately (the blue line price drops immediately after the deviation of the red line), making the deviation unprofitable. However, the punishment is not as harsh as it could be (i.e. reversion to the competitive price), and it is only temporary; afterwards, the algorithms gradually return to their pre-deviation prices.
…The collusion that we find is typically partial – the algorithms do not converge to the monopoly price but a somewhat lower one. However, we show that the propensity to collude is stubborn – substantial collusion continues to prevail even when the active firms are three or four in number, when they are asymmetric, and when they operate in a stochastic environment. The experimental literature with human subjects, by contrast, has consistently found that they are practically unable to coordinate without explicit communication save in the simplest case, with two symmetric agents and no uncertainty.
What is most worrying is that the algorithms leave no trace of concerted action – they learn to collude purely by trial and error, with no prior knowledge of the environment in which they operate, without communicating with one another, and without being specifically designed or instructed to collude.
Tacit collusion isn’t actually illegal since it’s virtually impossible to prove, at least among humans. Tacit collusion by AIs is going to be much more common but perhaps also easier to prove if the antitrust authorities can demand access to the algorithms. No need to torture the data when you can torture the AIs. It’s going to be a strange world.
Hat tip: Ankur Delight.