A One Parameter Equation That Can Exactly Fit Any Scatter Plot
In a very surprising paper Steven Piantadosi shows that a simple function of one parameter (θ) can fit any collection of ordered pairs {Xi,Yi} to arbitrary precision. In other words, the same simple function can fit any scatter plot exactly, just by choosing the right θ. The intuition comes from chaos theory. We know from chaos theory that simple functions can produce seemingly random, chaotic behavior and that tiny changes in initial conditions can quickly result in entirely different outcomes (the butterfly effect). What Piantadosi shows is that the space traversed in these functions by changing θ is so thick that you can reverse the procedure to find a function that fits any scatter plot. He gives two examples:
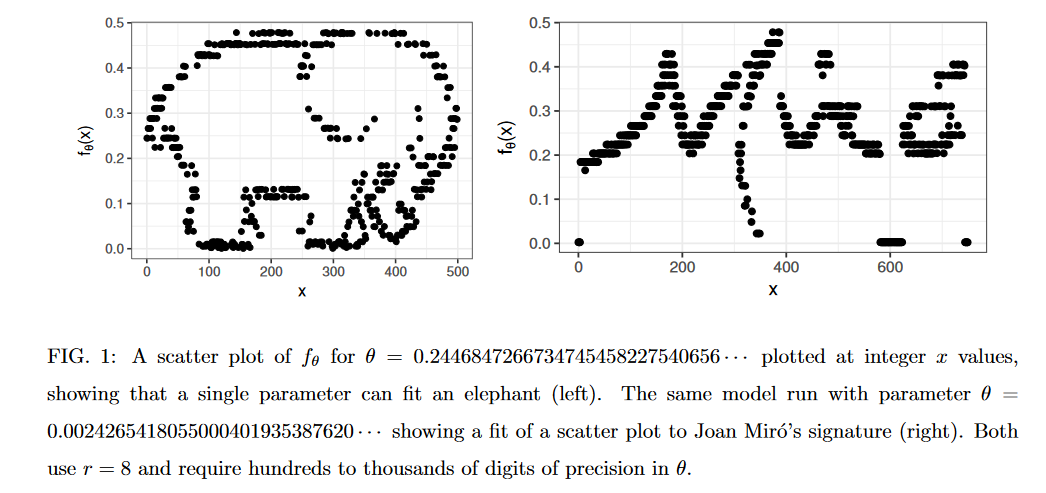
Note that he doesn’t present the actual θ’s used because they run to hundreds or thousands of digits. Moreover, if you are off by just one digit then you will quickly get a very different picture! Nevertheless, precisely because tiny changes in θ have big effects you can fit any scatter to arbitrary precision.
Aside from the wonderment at the result, the paper also tells us that Occam’s Razor is wrong. Overfitting is possible with just one parameter and so models with fewer parameters are not necessarily preferable even if they fit the data as well or better than models with more parameters. His conclusion is exactly right:
The result also emphasizes the importance of constraints on scientific theories that are enforced independently from the measured data set, with a focus on careful a priori consideration of the class of models that should be compared.