The Liberal Radicalism Mechanism for Producing Public Goods
 The mechanism for producing public goods in Buterin, Hitzig, and Weyl’s, Liberal Radicalism is quite amazing and a quantum leap in public-goods mechanism-design not seen since the Vickrey-Clarke-Groves mechanism of the 1970s. In this post, I want to illustrate the mechanism using a very simple example. Let’s imagine that there are two individuals and a public good available in quantity, g. The two individuals value the public good according to U1(g)=70 g – (g^2)/2 and U2(g)=40 g – g^2. Those utility functions mean that the public good has diminishing utility for each individual as shown by the figure at right. The public good can be produced at MC=80.
The mechanism for producing public goods in Buterin, Hitzig, and Weyl’s, Liberal Radicalism is quite amazing and a quantum leap in public-goods mechanism-design not seen since the Vickrey-Clarke-Groves mechanism of the 1970s. In this post, I want to illustrate the mechanism using a very simple example. Let’s imagine that there are two individuals and a public good available in quantity, g. The two individuals value the public good according to U1(g)=70 g – (g^2)/2 and U2(g)=40 g – g^2. Those utility functions mean that the public good has diminishing utility for each individual as shown by the figure at right. The public good can be produced at MC=80.
Now let’s solve for the private and socially optimal public good provision in the ordinary way. For the private optimum each  individual will want to set the MB of contributing to g equal to the marginal cost. Taking the derivative of the utility functions we get MB1=70-g and MB2= 40 – 2g (users of Syverson, Levitt & Goolsbee may recognize this public good problem). Notice that for both individuals, MB<MC, so without coordination, private provision doesn’t even get off the ground.
individual will want to set the MB of contributing to g equal to the marginal cost. Taking the derivative of the utility functions we get MB1=70-g and MB2= 40 – 2g (users of Syverson, Levitt & Goolsbee may recognize this public good problem). Notice that for both individuals, MB<MC, so without coordination, private provision doesn’t even get off the ground.
What’s the socially optimal level of provision? Since g is a public good we sum the two marginal benefit curves and set the sum equal to the MC, namely 110 – 3 g = 80 which solves to g=10. The situation is illustrated in the figure at left.
We were able to compute the optimum level of the public good because we knew each individual’s utility function. In the real world each individual’s utility function is private information. Thus, to reach the social optimum we must solve two problems. The information problem and the free rider problem. The information problem is that no one knows the optimal quantity of the public good. The free rider problem is that no one is willing to pay for the public good. These two problems are related but they are not the same. My Dominant Assurance Contract, for example, works on solving the free rider problem assuming we know the optimal quantity of the public good (e.g. we can usually calculate how big a bridge or dam we need.) The LR mechanism in contrast solves the information problem but it requires that a third party such as the government or a private benefactor “tops up” private contributions in a special way.
The topping up function is the key to the LR mechanism. In this two person, one public good example the topping up function is:
 Where c1 is the amount that individual one chooses to contribute to the public good and c2 is the amount that individual two chooses to contribute to the public good. In other words, the public benefactor says “you decide how much to contribute and I will top up to amount g” (it can be shown that (g>c1+c2)).
Where c1 is the amount that individual one chooses to contribute to the public good and c2 is the amount that individual two chooses to contribute to the public good. In other words, the public benefactor says “you decide how much to contribute and I will top up to amount g” (it can be shown that (g>c1+c2)).
Now let’s solve for the private optimum using the mechanism. To do so return to the utility functions U1(g)=70 g – (g^2)/2 and U2(g)=40 g – g^2 but substitute for g with the topping up function and then take the derivative of U1 with respect to c1 and set equal to the marginal cost of the public good and similarly for U2. Notice that we are implicitly assuming that the government can use lump sum taxation to fund any difference between g and c1+c2 or that projects are fairly small with respect to total government funding so that it makes sense for individuals to ignore any effect of their choices on the benefactor’s purse–these assumptions seem fairly innocuous–Buterin, Hitzig, and Weyl discuss at greater length.
Notice that we are solving for the optimal contributions to the public good exactly as before–each individual is maximizing their own selfish utility–only now taking into account the top-up function. Taking the derivatives and setting equal to the MC produces two equations with two unknowns which we need to solve simultaneously:
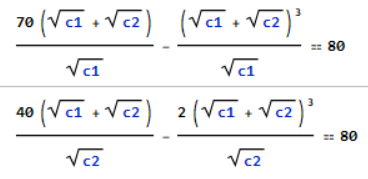
These equations are solved at c1== 45/8 and c2== 5/8. Recall that the privately optimal contributions without the top-up function were 0 and 0 so we have certainly improved over that. But wait, there’s more! How much g is produced when the contribution levels are c1== 45/8 and c2== 5/8? Substituting these values for c1 and c2 into the top-up function we find that g=10, the socially optimal amount!
In equilibrium, individual 1 contributes 45/8 to the public good, individual 2 contributes 5/8 and the remainder,15/4, is contributed by the government. But recall that the government had no idea going in what the optimal amount of the public good was. The government used the contribution levels under the top-up mechanism as a signal to decide how much of the public good to produce and almost magically the top-up function is such that citizens will voluntarily contribute exactly the amount that correctly signals how much society as a whole values the public good. Amazing!
Naturally there are a few issues. The optimal solution is a Nash equilibrium which may not be easy to find as everyone must take into account everyone else’s actions to reach equilibrium (an iterative process may help). The mechanism is also potentially vulnerable to collusion. We need to test this mechanism in the lab and in the field. Nevertheless, this is a notable contribution to the theory of public goods and to applied mechanism design.
Hat tip: Discussion with Tyler, Robin, Andrew, Ank and Garett Jones who also has notes on the mechanism.