Improving But Not Learning by Doing
In the excellent The Secret of Our Success Joe Henrich gives many examples of complex technological products and practices which were not the product of intelligence but rather of many, small, poorly understood improvements that were transmitted culturally down the generations. Derex et al. offer an ingenious experimental test of the cultural generation hypothesis.
Participants in the experiment were presented with a wheel with some weights that could be moved along four axis and they were asked to place the weights to maximize the speed at which the wheel moved down a track. The problem isn’t trivial since an optimal solution requires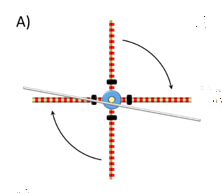 
placing the weights in different spots to take advantage of both inertial and potential energy. Participants were organized into chains of five. Each participant was given 5 trials. The weight configuration and the results of the last two trials were passed on to the next person in the chain. Thus, people farther down the chain potentially “inherit” more cultural knowledge.
What were the results? First, the average wheel speed increased down the generations from an average of 123.6 m/h for the final trial of the first generation/participant to 145.7 m/h by the last trial of the fifth generation. The researchers also tested whether participants improved their understanding of the causes of wheel speed by asking them to predict which of a series of wheel configurations would spin the fastest. If the faster speed of the fifth generation reflected learning by doing we would expect the fifth generation to make better predictions. In fact, there was no learning over time. Technology improved, understanding did not.
The authors then did an especially clever test. They allowed each generation/participant to leave the next generation a “theory” of wheel speed. Did this “book learning” speed up the evolution of technology? It did not. Moreover, theory transmission didn’t even result in much learning! Indeed, in some respects theories actually reduced learning because people who inherited a theory tended to believe it to the exclusion of other theories and, as a result, they reduced their exploration of the design space.
Of the 56 participants who received a theory… 15 received an inertia-related theory, 17 received an energy-related theory, 6 received a full theory and 18 received diverse, irrelevant theories
…inherited theories strongly affected participant’s understanding of the wheel system. Participants who did not inherit any theory (“Configurations” treatment) scored similarly (and better than chance) on questions about inertia and questions about energy (Fig. 3I). In comparison, participants who inherited an inertia- or energy- related theory showed skewed understanding patterns. Inheriting an inertia-related theory increased their understanding of inertia, but decreased their understanding of energy; symmetrically, inheriting an energy-related theory increased their understanding of energy, but decreased their understanding about inertia. One explanation for this pattern is that inheriting a unidimensional theory makes individuals focus on the effect of one parameter while blinding them to the effects of others. However, participants’ understanding may also result from different exploration patterns. For instance, participants who received an inertia-related theory mainly produced balanced wheels (Fig. 3F), which could have prevented them from observing the effect of varying the position of the wheel’s center of mass.
…These results suggest that the understanding patterns observed in participants who received unidimensional theories is likely the result of the canalizing effect of theory transmission on exploration. Note that in the present case, this canalizing effect is performance-neutral: with our 2-dimensional problem, better understanding of one dimension and worse understanding of one dimension simply compensate each other. For a many-dimensional problem, though, better understanding of one dimension is unlikely to compensate for worse understanding of all the others.
One aspect of knowledge transmission which is more difficult to study is the role of the genius. Cultural generation can get stuck in local optima. Only the genius can see over the valley to the mountain. The occasional genius may have been important even in knowledge generation in the pre-science era. In addition, these kinds of cultural evolution processes work best when feedback is quick and clear. Lengthen the time between input and output and all bets are off. Still this peculiar experiment illustrates how much cultural transmission can achieve and how theory can so dominate our thinking that it reduces vital experimentation.