Marty Weitzman’s Noah’s Ark Problem
Marty Weitzman passed away suddenly yesterday. He was on many people’s shortlist for the Nobel. His work is marked by high-theory applied to practical problems. The theory is always worked out in great generality and is difficult even for most economists. Weitzman wanted to be understood by more than a handful of theorists, however, and so he also went to great lengths to look for special cases or revealing metaphors. Thus, the typical Weitzman paper has a dense middle section of math but an introduction and conclusion of sparkling prose that can be understood and appreciated by anyone for its insights.
The Noah’s Ark Problem illustrates the model and is my favorite Weitzman paper. It has great sentences like these:
Noah knows that a flood is coming. There are n existing species/libraries, indexed i = 1, 2,… , n. Using the same notation as before, the set of all n species/libraries is denoted S. An Ark is available to help save some species/libraries. In a world of unlimited resources, the entire set S might be saved. Unfortunately, Noah’s Ark has a limited capacity of B. In the Bible, B is given as 300 x 50 x 30 = 450,000 cubits. More generally, B stands for the total size of the budget available for biodiversity preservation.
…If species/library i is boarded on the Ark, and thereby afforded some protection, its survival probability is enhanced to Pi. Essentially, boarding on the Ark is a metaphor for investing in a conservation project, like habitat protection, that improves survivability of a particular species/library. A particularly grim version of the Noah’s Ark Problem would make the choice a matter of life or death, meaning that Pi= 0 and Pi= 1. This specification is perhaps closest to the old testament version, so I am taking literary license here by extending the metaphor to less stark alternatives.
Weitzman first shows that the solution to this problem has a surprising property:
The solution of the Noah’s Ark Problem is always “extreme” in the following sense…In an optimal policy, the entire budget is spent on a favored subset of species/libraries that is afforded maximal protection. The less favored complementary subset is sacrificed to a level of minimal protection in order to free up to the extreme all possible scarce budget dollars to go into protecting the favored few.
Weitzman offers a stark example. Suppose there are two species with probabilities of survival of .99 and .01. For the same cost, we can raise the probability of either surviving by .01. What should we do?
We should save the first species and let the other one take its chances. The intuition comes from thinking about the species or libraries as having some unique features but also sharing some genes or books. When you invest in the first species you are saving the unique genes associated with that species and you are also increasing the probability of saving the genes that are shared by the two species. But when you put your investment in the second species you are essentially only increasing the probability of saving the unique aspects of species 2 because the shared aspects are likely saved anyway. Thus, on the margin you get less by investing in species 2 than by investing in species 1 even though it seems like you are saving the species that is likely to be saved anyway.
The math establishing the result is complex and, of course, there are caveats such as linearity assumptions which might reverse the example in a particular case but the thrust of the result is always operating: Putting all your eggs in one basket is a good idea when it comes to saving species.
Weitzman gets the math details right, of course!, but he knows that Noah isn’t a math geek.
Noah is a practical outdoors man. He needs robustness and rugged performance “in the field.” As he stands at the door of the ark, Noah desires to use a simple priority ranking list from which he can check off one species at a time for boarding. Noah wishes to have a robust rule….Can we help Noah? Is the concept of an ordinal ranking system sensible? Can there exist such a simple myopic boarding rule, which correctly prioritizes each species independent of the budget size? And if so, what is the actual formula that determines Noah’s ranking list for achieving an optimal ark-full of species?
So working the problem further, Weitzman shows that there is a relatively simple rule which is optimal to second-order, namely:
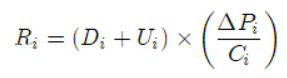
Where R is an index of priority. Higher R gets you on the ark, lower R bars entrance. D is a measure of a species distinctiveness–this could be measured, for example, by the nearest common ancestor metric. U is a measure of the special utility of a species beyond its diversity (Pandas are cute, goats are useful etc.) C is the cost of a project to increase the probability of survival and Delta P is the increase in the probability of survival so Delta P/C is the cost of increasing the probability of survival per dollar. Put simply we should invest our dollars where they have the most survival probability per dollar multiplied by a factor taking into account diversity and utility.
The rule is simple and sensible and and it has been used occasionally. Much more could be done, however, to optimize dollars spent on conservation and Weitzman’s rule gives us the necessary practical guidance. RIP.