Using Nature to Understand Nurture

An excellent new working paper uses genetic markers for educational attainment to track students through the 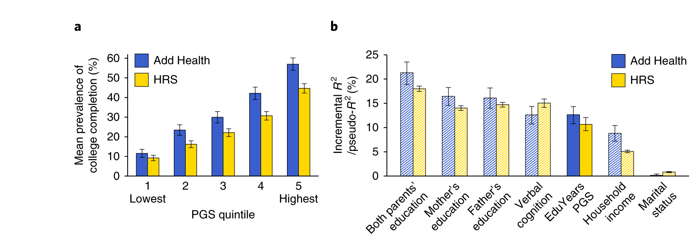high school math curriculum to better understand the role of nature, nurture and their interaction in math attainment. The paper begins with an earlier genome wide association study (GWAS) of 1.1 million people that found that a polygenic score could be used to (modestly) predict college completion rates. Panel (a) in the figure at right shows how college completion is five times higher in individuals with an education polygenic score (ed-PGS) in the highest quintile compared to individuals with scores in the lowest quintile; panel b shows that ed-PGS is at least as good as household income at predicting college attainment but not quite as good as knowing the educational level of the parents.

Of the million plus individuals with ed-PGS, some 3,635 came from European-heritage individuals who were entering US high school students in 1994-1995 (the Add Health sample). Harden, Domingue et al. take the ed-PGS of these individuals and match them up with data from their high school curricula and their student transcripts.

What they find is math attainment is a combination of nature and nurture. First, students with higher ed-PGS are more likely to be tracked into advanced math classes beginning in grade 9. (Higher ed-PGS scores are also associated with higher socio-economic status families and schools but these differences persist even after controlling for family and school SES or looking only at variation within schools.) Higher ed-PGS also predicts math persistence in the following years. The following diagram tracks high ed-PGS (blue) with lower ed-PGS (brown) over high school curricula/years and post high-school. Note that by grade 9 there is substantial tracking and some cross-over but mostly (it appears to me) in high-PGS students who fall off-track (note in particular the big drop off of blue students from Pre-Calculus to None in Grade 12).

Nature, however, is modified by nurture. “Students had higher returns to their genetic propensities for educational attainment in higher-status schools.” Higher ed-PGS students in lower SES schools were less likely to be tracked into higher-math classes and lower-SES students were less likely to persist in such classes.

It would be a mistake, however, to conclude that higher-SES schools are uniformly better without understanding the tradoffs. Lower SES schools have fewer high-ability students which makes it difficult to run advanced math classes. Perhaps the lesson here is that bigger schools are better, particularly bigger schools in poorer SES districts. A big school in a low SES district can still afford an advanced math curriculum.

The authors also suggest that more students could take advanced math classes. Even among the top 2% of students as measured by ed-PGS only 31% took Calculus in the high-SES schools and only 24% in the low SES schools.It’s not clear to me, however, that high-PGS necessitates high math achievement. Notice that many high-PGS students take pre-calc in Grade 11 but then no math in Grade 12 but they still go on to college and masters degrees. Lots of highly educated people are not highly-educated in math. Still it wouldn’t be a surprise if there were more math talent in the pool.

There is plenty to criticize in the paper. The measure of SES status by school (average mother’s educational attainment) leaves something to be desired. Moreover, there are indirect genetic effects, which the authors understand and discuss but don’t have the data to test. An indirect genetic effect occurs when a gene shared by parent and child has no direct effect on educational capacity (i.e. it’s not a gene for say neuronal development) but has an indirect “effect” because it is correlated with something that parent’s with that gene do to modify the environment of their children. Nevertheless, genes do have direct effects and this paper forces us to acknowledge that behavioral genetics has implications for policy.

Should every student be genotyped and tracked? On the one hand, that sounds horrible. On the other hand, it would identify more students of high ability, especially from low SES backgrounds. Genetics tells us something about a student’s potential and shouldn’t we try to maximize potential?

For homework, work out the equilibrium for inequality, rewatch the criminally underrated GATTACA and for an even more horrifying picture of the future, pay careful attention to the Mirrlees model of optimal income taxation.