Special Features of the Baumol Effect

I explained the Baumol effect in an earlier post based on Why Are the Prices So D*mn High?. In this post, I want to point out some special features of the Baumol effect that help to explain the data. Namely:

• The Baumol effect predicts that more spending will be accompanied by no increase in quality.
• The Baumol effect predicts that the increase in the relative price of the low productivity sector will be fastest when the economy is booming. i.e. the cost “disease” will be at its worst when the economy is most healthy!
• The Baumol effect cleanly resolves the mystery of higher prices accompanied by higher quantity demanded.

First, in the literature on rising prices it’s common to contrast massive increases in spending with little to no increases in quality, as for example, in contrasting education expenditures with mostly flat test scores (see at right). We have spent so much and gotten so little! Cui Bono? It must be teacher unions, administrators or the government!

All of that could be true but the Baumol effect predicts that more spending will be accompanied by no increase in quality. Go back to the classic example of the string quartet which becomes more expensive because labor in other industries increases in productivity over time. The price of the string quartet rises but does anyone expect that the the quality rises? Of course not. In the classic example the inputs to string quartet playing don’t change. The wages of the players rise because of productivity increases in other industries but we don’t invest any more real resources in string quartet playing and so we should not expect any increases in quality.

In just the same way, to the extent that greater spending on education, health care, or car repair is due to the rising opportunity costs of inputs we should not expect any increase in quality. (Note that increases in real resource use such as more teachers per student should result in increases in quality (and perhaps they do) but by eliminating the price increase portion of the higher spending we have eliminated a large portion of the mystery of higher spending with no increase in quality.)

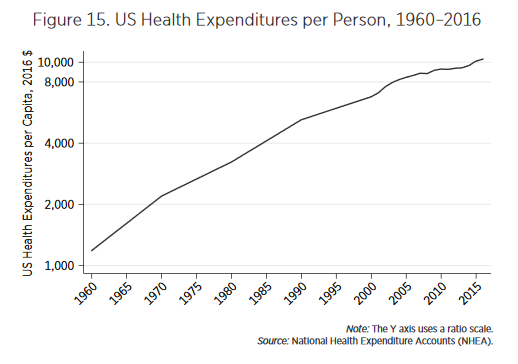Second, explanations of rising prices that focus on bad things such as monopoly power or rent seeking tend to imply that price increases should be largest when the economy is doing poorly. In contrast, the Baumol effect predicts that increases in relative prices will be largest when the economy is booming. Consider health care. From news reports you might think that health care costs have gotten more “out of control” over time. In fact, the fastest increases in health care costs were in the 1960s. The graph at left is on a ratio scale so slopes indicate rates of growth and what one sees is that the growth rate of health expenditures per person is slowing. That might seem good but remember, from the Baumol point of view, the decline in relative price growth reflects slowing growth elsewhere in the economy.

Third, holding all else equal, the only rational response to an ordinary cost increase is to substitute away from the good. But in many rising price sectors we see not only greater expenditures (driven by increased prices and inelastic demand) but also greater quantity demanded. As I showed earlier, for example, we have increased the number of doctors, nurses and teachers per capita even as prices have risen. John Cochrane correctly noted that this is puzzling but it’s a bigger puzzle for non-Baumol theories than for Baumol. For non-Baumol theories to explain increases in the quantity purchased, we need two theories. One theory to explain the increase in price (bloat/regulation etc.) and another theory to explain why, despite the increase in price, people are still purchasing more (e.g. income effect). The world is a messy place and maybe that is what is happening. But the Baumol effect offers a cleaner answer.

A Baumol increase in relative price is always accompanied by higher income so it’s much easier to explain how price increases can accompany increases in quantity as well as increases in expenditure. The Baumol story for increased purchase of medical care even as prices increase, for example, is no more mysterious than why people can take more leisure when wages increase–namely the higher wage means a higher income for any given hours and people choose to take some of this higher income in leisure. Similarly, higher productivity in say goods production increases income at any given production level and people choose to take some of this higher income in services.

Summing up, if we examine each sector–education, health care, the arts, etc.–on its own then there are always many possible explanations for why prices might be increasing. Many of these explanations have true premises–there are a lot of administrators in higher education, health care is highly regulated, lower education is government run. But, on closer inspection the arguments often don’t fit the data very well. Prices were increasing before administrators were important, health care is highly regulated but so is manufacturing, private education is also increasing in price, the arts are not highly regulated. It’s impossible to knock down each of these arguments in every industry, so there is always room for doubt. Indeed, the great difficult is that these factors often do result in higher costs and greater inefficiency but I believe those are predominantly level effects not effects that accumulate over time. Moreover, when one considers the rising price industries as a whole these explanations begin to look ad hoc. In contrast, the Baumol effect appears capable of explaining the pricing behavior of a wide variety of industries over a long period of time using a simple but powerful and unified theory.

Addendum: Other posts in this series.